La successione di Leonardo di Bonaccio, il Fibonacci da Pisa e il secondo principio della termodinamica o dell’entropia
 “Nella successione di Fibonacci, si legge in un articolo specifico sul web, matematico pisano del XIII secolo, ogni numero è il risultato della somma dei due precedenti: 0, 1, 1, 2, 3, 5, 8, 13… fino all’infinito. Fino al XIX secolo a questa successione non fu attribuita alcuna importanza, finché si scoprì che può essere applicata, per esempio, nel calcolo delle probabilità, nella sezione aurea e nel triangolo aureo.”
“Nella successione di Fibonacci, si legge in un articolo specifico sul web, matematico pisano del XIII secolo, ogni numero è il risultato della somma dei due precedenti: 0, 1, 1, 2, 3, 5, 8, 13… fino all’infinito. Fino al XIX secolo a questa successione non fu attribuita alcuna importanza, finché si scoprì che può essere applicata, per esempio, nel calcolo delle probabilità, nella sezione aurea e nel triangolo aureo.”
Troviamo la sequenza del matematico pisano in diversi ambiti naturali e “culturali”, cioè in opere umane, come ad esempio nei fregi presenti su facciate di diverse chiese, tra cui San Nicola a Pisa. La troviamo in musica, sia in quella classica, da J. S. Bach alla contemporanea di Karheinz Stockausen, sia nel rock, come nel favoloso brano dei Deep Purple Child in time, e di più ancora nel progressive dei Genesis.
Fermandoci un momento ai fregi di San Nicola il professor Armienti la pensa in questo modo:
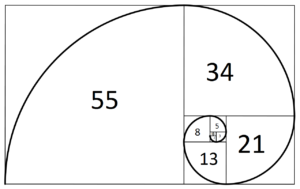
“(…) le eleganti simmetrie dell’opera sono un richiamo diretto alle scoperte del matematico pisano, poiché se si assume come unitario il diametro dei cerchi più piccoli dell’intarsio, i più grandi hanno diametro doppio, i successivi triplo, mentre quelli di diametro 5 sono divisi in spicchi nei quadratini ai vertici del quadrato in cui è inscritto il cerchio principale, quello centrale ha diametro 13 mentre il cerchio che circoscrive i quadratini negli angoli ha diametro 8. Gli altri elementi dell’intarsio disposti secondo tracce circolari individuano circonferenze di raggio 21 e 34, infine il cerchio che circoscrive l’intarsio ha diametro 55 volte più grande del circolo minore. 1,2,3,5,8,13,21,34,55 sono i primi nove elementi della successione di Fibonacci“.
La successione di Fibonacci è un teorema matematico, collegato a molti altri, che conferma come la natura sia leggibile con strumenti matematici, come già sapevano Egizi e Mesopotamici, Euclide e Pitagora, Arabi ed Europei, Eulero, Riemann e Goedel, fino ai nostri giorni.
Fiori e infiorescenze, coralli e molluschi attestano la presenza di questa forma affascinante, confermando in qualche modo come la Natura ubbidisca a una superiore razionalità, che dà da pensare anche oltre l’oggetto dei suoi argomenti.
La geometria di intere piante, fiori o frutti, mostra con evidenza strutture e forme ricorrenti. Un esempio efficace si può trarre dal numero di petali dei fiori; la maggior parte ne ha 3 (come gigli e iris), 5 (ranuncoli, rose canine, plumeria), oppure 8, 13 (alcune margherite), 21 (cicoria), 34, 55 o 89 (asteracee). Anche questi numeri fanno parte della successione di cui stiamo parlando, in cui ciascun numero equivale alla somma dei due precedenti: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
Una significativa caratteristica della sequenza mette in evidenza che il rapporto tra qualunque numero e quello precedente nella serie tenda verso un valore ben definito: 1,618… . Si tratta del numero aureo o sezione aurea, ϕ (Phi), presente, come abbiamo visto, sia in natura sia in opere architettoniche costruite dall’uomo, come i fregi di San Nicola in Pisa o le stesse piramidi egizie. Nelle piante con foglie disposte a spirale, per ogni giro attorno al fusto ci sono in media Phi foglie, fiori o petali. Ciò significa che, girando attorno ad uno stelo e muovendosi dal basso verso l’alto, incontreremo una foglia o un fiore ogni 222,5°, valore che si ottiene dividendo l’angolo giro di 360° per Phi.
E mi fermo qui perché non sono un matematico. Occupandomi però di filosofia, non posso non notare come la trattazione della successione di Fibonacci possa fare venire in mente una legge fisica tra le più famose, la seconda della termodinamica, che si esprime anche con il concetto di entropia.
Il termine deriva dal greco antico ἐν en, “dentro”, e τροπή tropé, “trasformazione”, e significa una grandezza interpretabile come misura del disordine presente in un sistema fisico qualsiasi, incluso, compreso l’universo. Viene generalmente rappresentata dalla lettera S e nel Sistema Internazionale si misura in joule fratto kelvin (J/K).
In termodinamica classica, il primo ambito in cui l’entropia fu introdotta, come S, è stata una funzione di stato di un sistema in equilibrio termodinamico. Pertanto, si può dire che quando un sistema passa da uno stato di equilibrio ordinato a uno disordinato la sua entropia aumenta.
Il termine e il concetto di entropia è stato successivamente esteso ad ambiti non strettamente fisici, come le scienze sociali e la teoria dell’informazione. Semplificando molto, e io sono in grado di fare solo questo, perché non sono neanche un fisico, ma poi si capirà la ragione per cui mi sono imbarcato in questo argomento, si può anche affermare che l’entropia interpreta il “grado di disordine” di un sistema.
Se aumenta il disordine aumenta l’entropia, dunque, e ciò funziona anche all’incontrario. Ad esempio, si potrebbe proporre una visualizzazione dell’aumento di entropia in un sistema, raffigurando l’aumento di incompetenza e cioè di ignoranza-ignorante. In strutture organizzate (più o meno) come le aziende di produzione o di servizi ciò può risultare evidente dai dati di un’analisi del clima ben condotta, là dove gli item scelti siano sufficienti a rappresentare l’agio o il disagio crescenti o in calo del sentiment dei partecipanti-protagonisti, di solito i lavoratori.’
La presenza di una situazione entropica si può dunque registrare e segnalare, per predisporre opportuni rimedi che possono essere formazione mirata e counseling. A questo punto possiamo senz’altro intuire come sia lecito collegare in qualche modo la razionale e armoniosa successione di Fibonacci che mostra una crescita progressiva, esteticamente elegante, e il sopraggiungere di una situazione entropica, che deve essere riconosciuta per tempo, onde evitare guai maggiori all’organizzazione e alla produttività, nonché allo stato di agio psicologico e morale dei partecipanti.
Se da una lato la sequenza di Fibonacci ci può ispirare fiducia nel progressivo miglioramento dello stato mentale e fisico dei partecipanti, il secondo principio della termodinamica ci evidenzia, come in una dolorosa metafora, ciò che da u-topia iniziale del creativo start-upper, può diventare dis-topia, vale a dire modo e senso di marcia errato, o addirittura retro-topia (cf. Zygmund Bauman), cioè un agire rivolto allo sterile rimpianto del passato.
E’ bellissimo che la matematica e la fisica, se opportunamente studiate, possano aiutare efficacemente i saperi antropologici preposti alla gestione delle risorse umane e alla loro crescita, sia sotto il profilo personale, sia professionale. Mai stancarsi di studiare, cara lettrice e caro lettore.
Post correlati

0 Comments